How to Calculate Torque: Your Complete Guide
This comprehensive guide will walk you through the process of calculating torque, explaining the necessary formulas and concepts along the way.
Photo by ThisisEngineering on Unsplash
This article was first published on
www.botasys.comTorque is a fundamental concept in physics and engineering that describes the rotational force applied to an object. Understanding how to calculate torque is crucial in various applications, from designing engines to constructing buildings.
This comprehensive guide will walk you through the process of calculating torque, explaining the necessary formulas and concepts along the way.
Understanding Torque
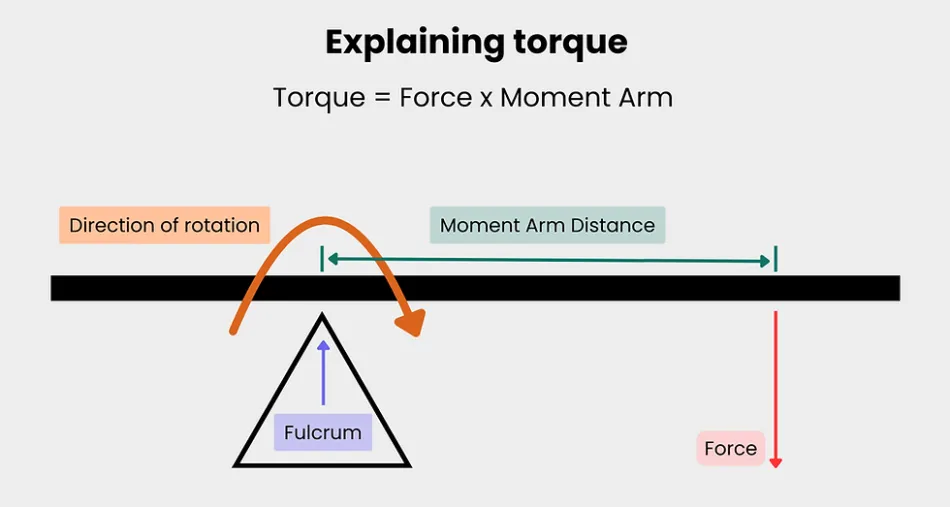
Torque, often referred to as the moment of force, measures the tendency of a force to rotate an object about an axis. It plays a crucial role in mechanical systems, influencing how objects spin and rotate.
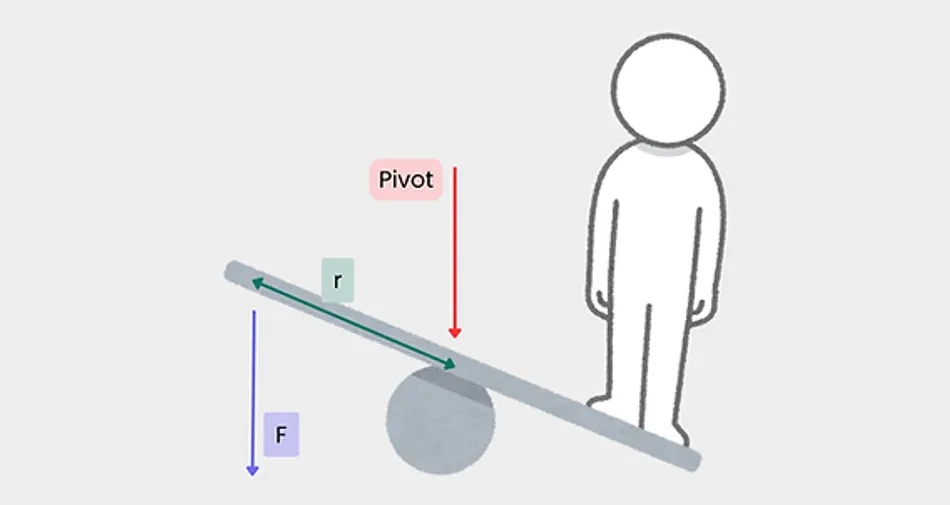
The unit of torque in the International System of Units (SI) is the Newton-meter (Nm). Imagine a seesaw. The force you apply as your weight and the distance you sit from the pivot point determine how easily the seesaw tilts.
This principle applies to all situations involving torque. The greater the force applied and the farther it's exerted from the pivot point, the greater the torque produced.
How to Calculate Torque
Let's first look at the torque formula and then move on to some solved examples that illustrate how to calculate torque using the torque equation.
The Torque Formula
The formula for calculating torque is:
τ (torque) = F (force) × r (lever arm) × sin(θ)
Where:
τ (tau) represents torque (measured in newton-meters, N⋅m)
F (force) represents the magnitude of the force applied (measured in newtons, N)
r (lever arm) represents the distance from the fulcrum/pivot point to the point where the force is applied (measured in meters, m)
θ (theta) represents the angle between the force vector and the lever arm (measured in degrees or radians)
The lever arm is the perpendicular distance between the line of action of the force and the pivot point. It's essentially the effective distance at which the force acts. The angle between the force and the lever arm significantly affects the torque.
A force applied perpendicularly (θ = 90°) produces the maximum torque. As the angle decreases, the torque reduces to zero when the force acts along the lever arm (θ = 0°).
Examples of Torque Calculations
Here are a few examples that explain how to calculate torque.
Example 1: Perpendicular Force
Suppose you apply a force of 10 N at the end of a 0.5-meter wrench. The angle between the force and the lever arm is 90°.
Solution:
𝜏=𝑟×𝐹
𝜏=0.5 m×10 N
𝜏=5 Nm
Example 2: Tightening a Lug Nut
Imagine you're tightening a lug nut on a car tire with a wrench 0.5 meters long. You apply a force of 50 N at an angle of 30° to the handle. Find the torque applied to the lug nut?
Solution:
τ = 50 N × 0.5 m × sin(30°)
τ ≈ 12.5 N⋅m
Example 3: Seesaw Balance
Two children of different weights are playing on a seesaw.
One child weighing 40 kg sits 2 meters from the fulcrum, while the other weighing 30 kg sits 3 meters away. To balance the seesaw, what distance from the fulcrum should the lighter child move to?
Solution:
We can set up a torque equation for each child:
Child 1: τ₁ = 40 kg × 9.8 m/s² (gravity) × 2 m
Child 2: τ₂ = 30 kg × 9.8 m/s² × 3 m (assuming constant gravity)
For the seesaw to balance, the torques must be equal (τ₁ = τ₂). Solve for the distance (d) the lighter child needs to move:
d = (τ₁ × 3 m) / (30 kg × 9.8 m/s²) ≈ 2.65 m
Note: Don’t forget to convert units appropriately (e.g., weight to force) when applying the torque formula.
Example 4: Torque in a Car Engine
Imagine a scenario where you need to calculate the torque produced by a car engine. The engine applies a force to a crankshaft, which in turn causes rotation that ultimately powers the wheels of the vehicle.
How can we calculate the torque produced by a car engine that applies a force of 1500 Newtons to a crankshaft, where the distance from the center of the crankshaft to the point where the force is applied is 0.1 meters? Assume the force is applied tangentially to the crankshaft.
Solution:
The torque formula is given by:
𝜏=𝑟×𝐹×sin(𝜃)
Since the angle 𝜃 is 90°, sin(90°)=1:
𝜏=0.1 m×1500 N×sin(90∘)
τ𝜏=0.1 m×1500 N×1
𝜏=150 Nm
Example 5:Rotational Torque in a Robotic Arm
Problem:
A robotic arm applies a force of 200 Newtons at the end of its 0.5-meter-long segment. The force is applied at an angle of 60 degrees to the arm. How can we calculate the torque produced by this force?
Solution:
The torque formula is:
𝜏=𝑟×𝐹×sin(𝜃))
Calculate sin(60∘), which is 3/2≈0.866
𝜏=0.5 m×200 N×sin(60∘)
𝜏=0.5 m×200 N×0.866
𝜏=100×0.866
τ=86.6Nm
Additional Considerations
Torque as a Vector Quantity: While the formula illustrates how to find the magnitude of torque, torque is also a vector quantity with direction. The right-hand rule can be used to determine the direction of torque.
Average Torque: In situations where the force or angle varies, you might need to calculate the average torque over time.
Practical Applications
Torque calculation is essential in various fields. Here are a few examples that show the importance of knowing how to calculate torque in Engineering Design:
Automotive Engineering: Determining the torque output of engines.
Structural Engineering: Ensuring stability in structures by calculating the torque on beams and supports.
Mechanical Design: Designing and analyzing the performance of machinery and tools.
Robotics: Ensuring precise and reliable movements.
Measuring Torque
Measuring torque is essential for ensuring the accuracy and reliability of various mechanical systems.
This involves using tools like torque wrenches, which apply a specific torque to fasteners, and force-torque sensors, which measure the torque in both static and rotating systems such as engines and robotic arms.
Accurate torque measurement helps in preventing mechanical failures, optimizing performance, and ensuring safety in applications ranging from automotive engines to robotic arms. Properly calibrated torque measurement tools are crucial for maintaining the integrity and efficiency of engineered systems.
Estimating Torque by Hand
In some practical situations, precise torque measurements might not be feasible. Estimating torque by hand involves applying known forces at known distances, using calibrated tools like torque wrenches to ensure accuracy.
Conclusion
By understanding the concept of torque and its formula, you can solve problems involving rotational motion and forces.
This knowledge can be applied in various real-world scenarios, from simple tasks like tightening a screw to complex engineering applications.
So, the next time you use a wrench or witness a machine in action, remember the invisible force of torque at play!